1
丸ビルの地下のスターバックスでコーヒーでも飲んでひと休みしようと思ったら、 入口近くの席しかあいてなかった。 自動ドアが開いたり閉まったりでせわしない。 あまりに落ち着けないので、やむなく、出入りする客を数えてみた。 昔ながらの「正」の字でカウント。

J.L.ベントリー著「プログラマのうちあけ話」 (more programming pearls) でリトルの法則なるものが紹介されている。 リトルの法則とは以下のようなもの。
システム内にある事物の平均個数(N)は事物がシステムから出ていく平均の割合(X)とそれぞれがシステムの中で費やす平均時間(Z)を乗じたものである (N = X × Z)
ということで、スタバの客一人当たりの平均滞在時間 Z は、 店内の座席数 を N、 単位時間内に店から出た人数を X とすると、N÷X で求められる。 実際に数えると、N ≒ 35 (席)、X ≒ 100 (人/時間)。 これらを基に計算してみると、 35÷100×60 で、平均滞在時間は約 20 分。 まあ、こんなもんかな、と。 一人で来る若い女性は、コーヒー買って、座って、 飲みながら携帯でメール打って、そそくさと出ていっちゃうものね。
2
リトルの法則は、いわゆる「はじき」の法則と同じ。 個数(N)が距離に、出ていく割合(X)が速さに対応している。 はじきの法則とは、速さ・時間・距離の関係を覚えるためのもの。 こんな図で覚える。
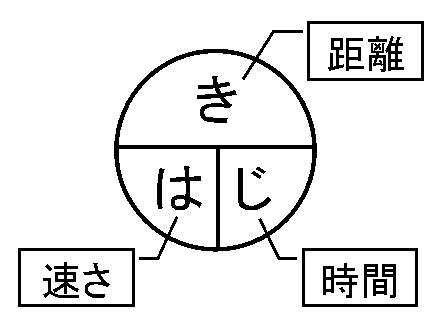
速さを計算する式を知りたかったら、「は」を指で隠すと、あら不思議、 「き」が分子で「じ」が分母の分数、 つまり「速さ=距離÷時間」となるのが分かる。 距離を計算するには「き」を指で隠して、「は」×「じ」。なつかしいね。